Rainfall Anomaly Index

Based on van Rooy, M.P. (1965). A Rainfall Anomaly Index Independent of Time and Space. Notos.

Packages

import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd

from spei.rai import mrai, rai

Data

df = pd.read_csv("data/DEBILT.csv", index_col=0, parse_dates=True)
prec = df["Prec [m/d] 260_DEBILT"].multiply(1e3).resample("MS").sum()

Calculate Index

ra_index = rai(prec)
mra_index = mrai(prec, sf=1.7)

Visualize

f, ax = plt.subplots(2, 1, figsize=(12, 6), sharex=True, sharey=True)
ax[0].plot(ra_index.index, ra_index.values, color="C0")
ax[1].plot(mra_index.index, mra_index.values, color="C1")
ax[0].set_ylabel("Rainfall Anomaly Index")
ax[1].set_ylabel("Modified Rainfall Anomaly Index")
ax[0].grid(True)
ax[1].grid(True)
ax[1].yaxis.set_major_locator(mpl.ticker.MultipleLocator(1))
ax[1].xaxis.set_major_locator(mpl.dates.YearLocator(1))
ax[1].set_xlim(pd.Timestamp("2010-01-01"), pd.Timestamp("2020-12-31"))

(np.float64(14610.0), np.float64(18627.0))

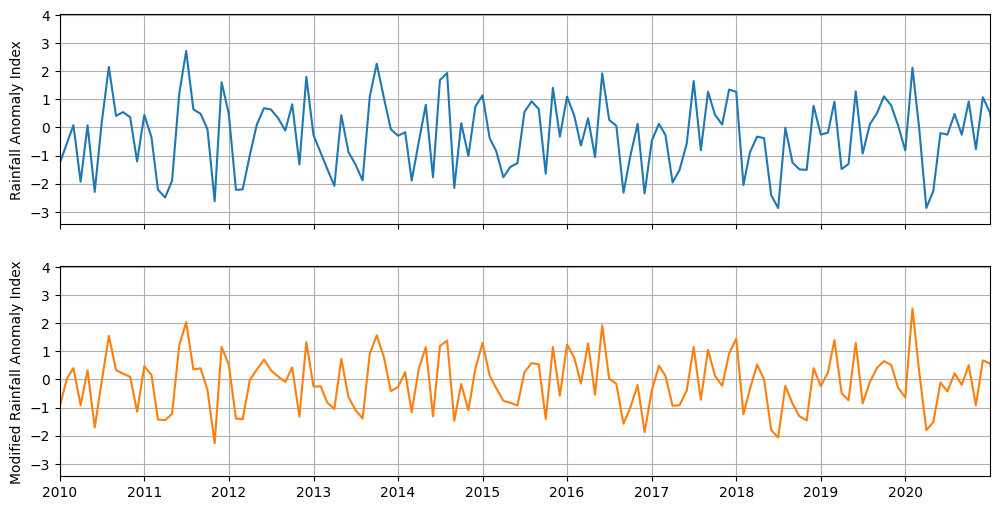
Interpretation based on Hansel (2015) - The Modified Rainfall Anomaly Index (mRAI)

RAI	Description	mRAI	Description
\(\ge\) 3.00	Extremely wet	\(\ge\) 2.00	Extremely wet
2.00 to 2.99	Very wet	1.50 to 1.99	Very wet
1.00 to 1.99	Moderately wet	1.00 to 1.49	Moderately wet
0.50 to 0.99	Slightly wet	0.50 to 0.99	Slightly wet
-0.49 to 0.49	Near normal	-0.49 to 0.49	Near normal
-0.99 to -0.50	Slightly dry	-0.99 to -0.50	Slightly dry
-1.99 to -1.00	Moderately dry	-1.49 to -1.00	Moderately dry
-2.99 to -2.00	Very dry	-1.99 to -1.50	Very dry
≤-3.00	Extremely dry	≤-2.00	Extremely dry