Drought Prediction with Time Series Modeling

Martin Vonk - 2022

This notebooks shows a quick calculation of the SPI, SPEI and SGI for De Bilt, in the Netherlands. The SGI is calculated using a Pastas time series model since the original time series is too short. The application of time series models for extrapolating groundwater time series is discussed in Brakkee et al (2022).

Required packages

import matplotlib.pyplot as plt
import pandas as pd
import pastas as ps
import scipy.stats as scs

import spei as si  # si for standardized index

print(si.show_versions())

python: 3.11.14
spei: 0.8.1
numpy: 2.3.5
scipy: 1.16.3
matplotlib: 3.10.8
pandas: 2.3.3

Import time series

Time series are imported using the package hydropandas. Enddate is by default yesterday. The head time series is obtained from a Pastas test dataset.

# import hydropandas as hpd

# today = datetime.date.today()
# yesterday = (today - datetime.timedelta(days=1)).strftime("%Y-%m-%d")
# prec = (
#     hpd.PrecipitationObs.from_knmi(
#         meteo_var="RH", stn=260, startdate="1959-07-01", enddate=yesterday
#     )
#     .multiply(1e3)
#     .squeeze()
# )
# prec.index = prec.index.normalize()
# evap = (
#     hpd.EvaporationObs.from_knmi(
#         meteo_var="EV24", stn=260, startdate="1959-07-01", enddate=yesterday
#     )
#     .multiply(1e3)
#     .squeeze()
# )
# evap.index = evap.index.normalize()


df = pd.read_csv("data/DEBILT.csv", index_col=0, parse_dates=True)
prec = df["Prec [m/d] 260_DEBILT"].multiply(1e3).rename("prec")
evap = df["Evap [m/d] 260_DEBILT"].multiply(1e3).rename("evap")
head = df["Head [m] B32C0572_DEBILT"].rename("B32C0572").dropna()
today = df.index[-1]
yesterday = df.index[-2]

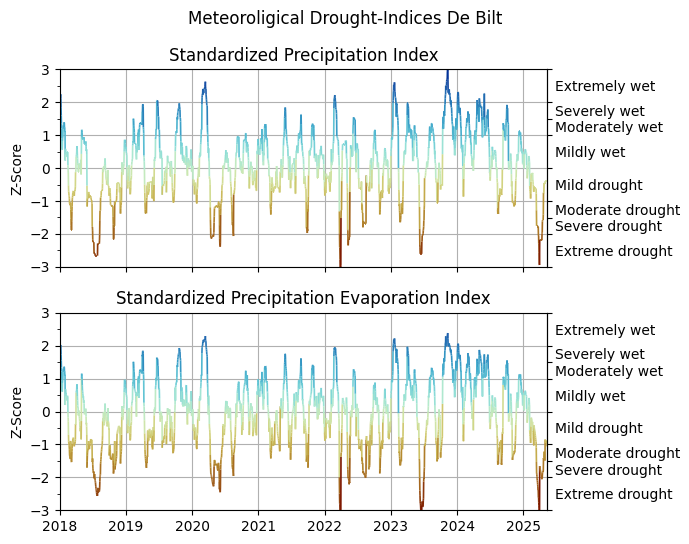
Calculate SPI and SPEI

# Accumulate time series on monthly basis
spi1 = si.spi(prec, timescale=30, dist=scs.gamma, fit_freq="MS")
spei1 = si.spei((prec - evap), timescale=30, dist=scs.fisk, fit_freq="MS")

xlim = pd.to_datetime(["2018-01-01", df.index[-1]])

fig, axs = plt.subplots(2, 1, figsize=(7.0, 5.5), sharex=True)
si.plot.si(spi1, ax=axs[0], background=False, cmap="roma")
si.plot.si(spei1, ax=axs[1], background=False, cmap="roma")
[(x.grid(), x.set_xlim(xlim), x.set_ylabel("Z-Score")) for x in axs]
axs[0].set_title("Standardized Precipitation Index")
axs[1].set_title("Standardized Precipitation Evaporation Index")
fig.suptitle("Meteoroligical Drought-Indices De Bilt")
fig.tight_layout()

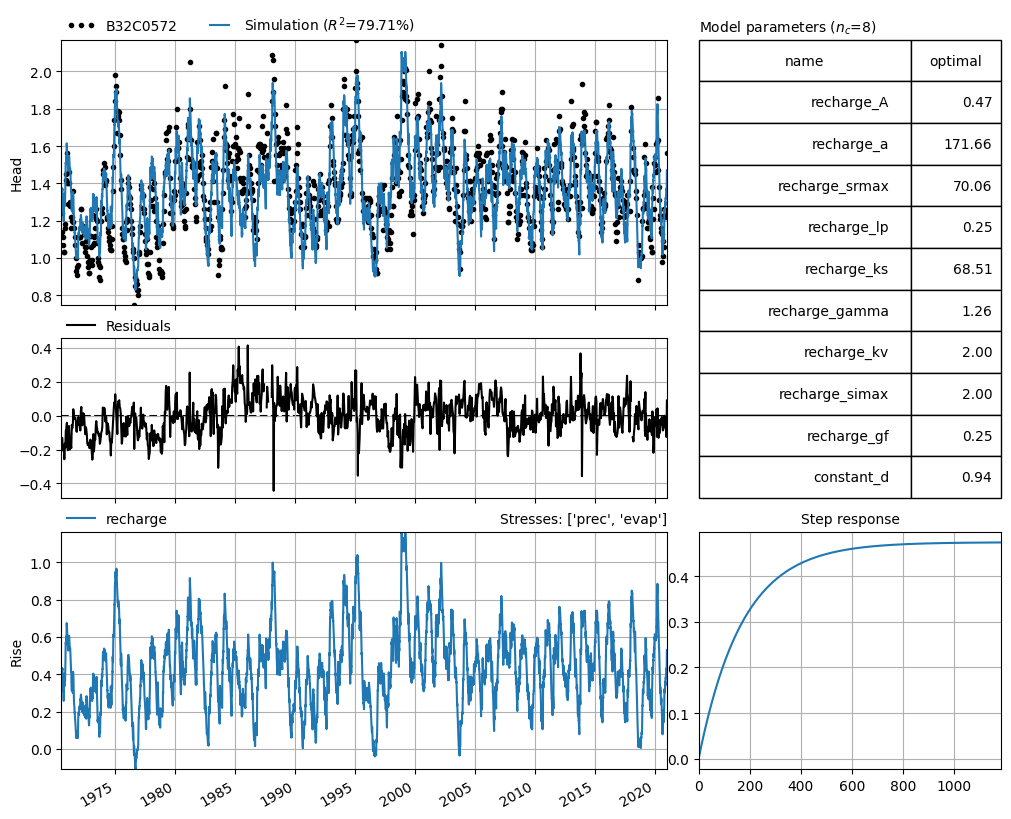
Create time series model and simulate head

ml = ps.Model(head)
rm = ps.RechargeModel(
    prec, evap, ps.Exponential(), recharge=ps.rch.FlexModel(gw_uptake=True)
)
ml.add_stressmodel(rm)
ml.solve(tmin="1970-07-01", report=True)
_ = ml.plots.results(figsize=(10.0, 8.0))

Fit report B32C0572                 Fit Statistics
==================================================
nfev     45                     EVP          79.61
nobs     1187                   R2            0.80
noise    False                  RMSE          0.11
tmin     1970-07-01 00:00:00    AICc      -5305.21
tmax     2020-12-28 00:00:00    BIC       -5264.70
freq     D                      Obj           6.71
freq_obs None                   ___
warmup   3650 days 00:00:00     Interp.         No
solver   LeastSquares           weights        Yes

Parameters (8 optimized)
==================================================
                   optimal     initial   vary
recharge_A        0.468697    0.443936   True
recharge_a      170.731185   10.000000   True
recharge_srmax  103.744124  250.000000   True
recharge_lp       0.250000    0.250000  False
recharge_ks     145.327844  100.000000   True
recharge_gamma    1.470452    2.000000   True
recharge_kv       1.999723    1.000000   True
recharge_simax    2.000000    2.000000  False
recharge_gf       0.250354    1.000000   True
constant_d        0.950055    1.377665   True

Calculate SGI based on time series model

gws = ml.simulate(tmin="1990-07-01", tmax=yesterday)
sgi = si.sgi(gws, fit_freq="MS")

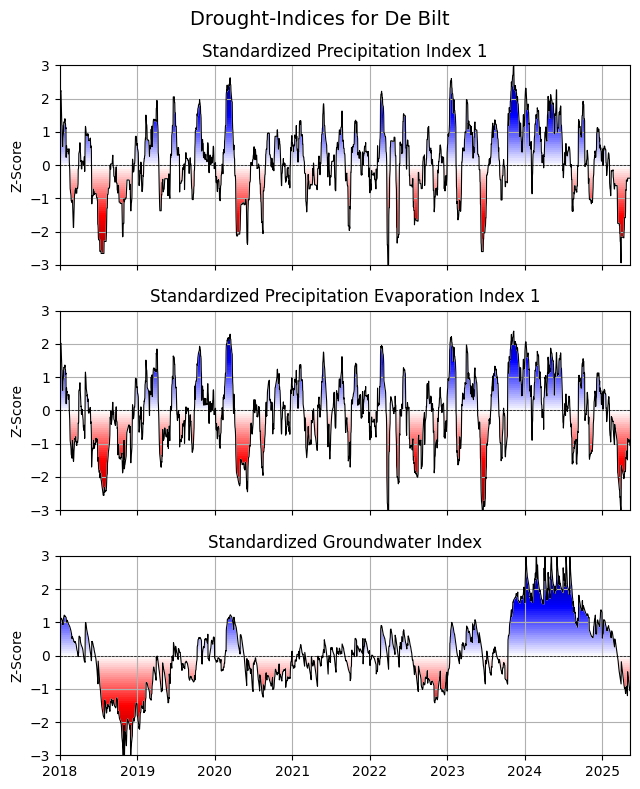
Compare three drought-indices (SPI, SPEI, SGI) in plot

fig, axs = plt.subplot_mosaic(
    [["SPI"], ["SPEI"], ["SGI"]], figsize=(6.5, 8), sharex=True
)
si.plot.si(spi1, ax=axs["SPI"], add_category=False)
si.plot.si(spei1, ax=axs["SPEI"], add_category=False)
si.plot.si(sgi, ax=axs["SGI"], add_category=False)
[(axs[x].grid(), axs[x].set(xlim=xlim, ylabel="Z-Score")) for x in axs]
axs["SPI"].set_title("Standardized Precipitation Index 1")
axs["SPEI"].set_title("Standardized Precipitation Evaporation Index 1")
axs["SGI"].set_title("Standardized Groundwater Index")
fig.suptitle("Drought-Indices for De Bilt", fontsize=14)
fig.tight_layout()
# fig.savefig('Drought_Index_Bilt.png', dpi=600, bbox_inches='tight')

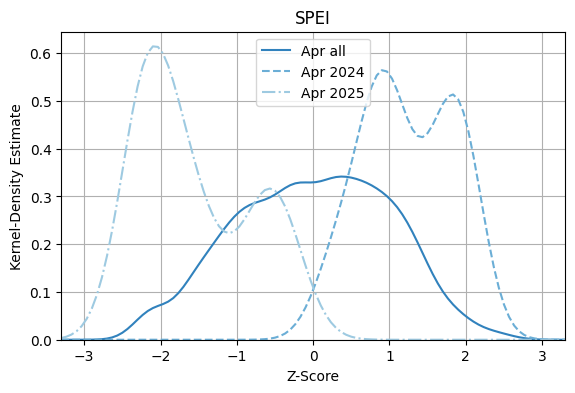
Compare SPEI Kernel Density Estimate for one month

ax = si.plot.monthly_density(
    spi1, years=[today.year - 1, today.year], months=[today.month - 1]
)
ax.set_xlabel("Z-Score")
ax.set_title("SPEI");